En el ámbito de la estadística y el análisis de datos, la desviación estándar es una medida clave que nos permite comprender la dispersión de un conjunto de valores con respecto a su media. En el mundo actual, donde la recopilación y el análisis de datos son fundamentales en numerosos campos, el dominio de herramientas como Excel se vuelve esencial.
Excel, la popular hoja de cálculo desarrollada por Microsoft, ofrece una amplia gama de funciones estadísticas que simplifican el proceso de cálculo de la desviación estándar. Mediante el uso de fórmulas y funciones predefinidas, es posible obtener resultados precisos y rápidos.
En este artículo, exploraremos paso a paso cómo calcular la desviación estándar en Excel. Comenzaremos por explicar qué es la desviación estándar y por qué es importante en el análisis de datos. Luego, aprenderemos cómo utilizar la función DESVEST en Excel para calcular la desviación estándar de un conjunto de valores.
Además, exploraremos otras funciones relacionadas, como DESVEST.P y DESVEST.M, que nos permiten calcular la desviación estándar poblacional y la desviación estándar muestral, respectivamente. Estas variantes son útiles en diferentes contextos y nos brindan información adicional sobre la distribución de los datos.
Finalmente, proporcionaremos ejemplos prácticos y consejos para el manejo de errores comunes al calcular la desviación estándar en Excel. Con esta guía completa, estarás preparado para enfrentar cualquier desafío estadístico que se te presente y aprovechar al máximo las capacidades de Excel.
Cómo se calcula la desviación estándar en Excel
La desviación estándar es una medida estadística que nos permite conocer qué tan dispersos están los datos con respecto a la media. En Excel, calcular la desviación estándar es muy sencillo y se puede realizar de varias formas.
Utilizando la función EST.DEV
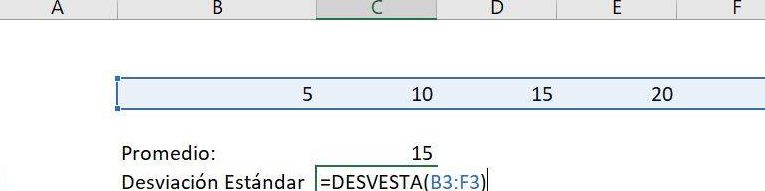
Una forma de calcular la desviación estándar en Excel es utilizando la función EST.DEV. Esta función nos permite calcular la desviación estándar de un conjunto de datos.
Para utilizar la función EST.DEV, simplemente debemos seleccionar el rango de datos del cual queremos calcular la desviación estándar y escribir la fórmula =EST.DEV(rango_de_datos).
Por ejemplo, si tenemos los datos en la columna A desde la celda A1 hasta la celda A10, la fórmula sería =EST.DEV(A1:A10).
Utilizando la función DESVESTP
Otra forma de calcular la desviación estándar en Excel es utilizando la función DESVESTP. Esta función también nos permite calcular la desviación estándar de un conjunto de datos.
Para utilizar la función DESVESTP, al igual que con la función EST.DEV, debemos seleccionar el rango de datos del cual queremos calcular la desviación estándar y escribir la fórmula =DESVESTP(rango_de_datos).
Por ejemplo, si tenemos los datos en la columna A desde la celda A1 hasta la celda A10, la fórmula sería =DESVESTP(A1:A10).
Utilizando la fórmula manualmente
También es posible calcular la desviación estándar en Excel utilizando la fórmula manualmente.
La fórmula para calcular la desviación estándar es la siguiente:
√(Σ(x – μ)² / N)
Donde:
- x representa cada valor individual del conjunto de datos.
- μ representa la media del conjunto de datos.
- N representa el número total de datos.
Para calcular la desviación estándar manualmente, debemos seguir los siguientes pasos:
- Calcular la media de los datos.
- Restar cada valor individual de la media y elevarlo al cuadrado.
- Sumar todos los valores obtenidos en el paso anterior.
- Dividir la suma obtenida entre el número total de datos.
- Calcular la raíz cuadrada del resultado obtenido en el paso anterior.
Estos son los diferentes métodos que se pueden utilizar para calcular la desviación estándar en Excel. Es importante tener en cuenta que la desviación estándar nos brinda información acerca de la dispersión de los datos, lo cual puede ser útil en análisis estadísticos y en la toma de decisiones.
Cómo sacar la desviación estándar fórmula
Calcular la desviación estándar en Excel es una tarea sencilla y útil para analizar la variabilidad de un conjunto de datos. La desviación estándar es una medida estadística que nos indica qué tan dispersos están los datos con respecto a la media. A continuación, te explicaré cómo sacar la desviación estándar utilizando la fórmula en Excel.
Paso 1: Organiza tus datos
Lo primero que debes hacer es organizar tus datos en una columna de Excel. Asegúrate de que los datos estén en una sola columna y que no haya celdas vacías entre ellos. Por ejemplo:
- Datos:
- 5
- 8
- 3
- 6
- 9
Paso 2: Calcula la media
El siguiente paso es calcular la media de tus datos utilizando la fórmula =PROMEDIO() de Excel. Esta función te dará el valor promedio de los datos. Por ejemplo:
=PROMEDIO(A1:A5)
Paso 3: Calcula la diferencia entre cada dato y la media
Ahora, debes calcular la diferencia entre cada dato y la media utilizando la fórmula =A1-MEDIA(A1:A5). Esta fórmula te dará la diferencia entre el valor de cada dato y la media. Por ejemplo:
=A1-MEDIA(A1:A5)
Paso 4: Calcula el cuadrado de cada diferencia
El siguiente paso es calcular el cuadrado de cada diferencia utilizando la fórmula =((A1-MEDIA(A1:A5))^2). Esta fórmula te dará el cuadrado de cada diferencia. Por ejemplo:
=((A1-MEDIA(A1:A5))^2)
Paso 5: Calcula la suma de los cuadrados de las diferencias
Una vez que hayas calculado el cuadrado de cada diferencia, debes sumar todos los cuadrados utilizando la fórmula =SUMA() de Excel. Esta función te dará la suma de los cuadrados de las diferencias. Por ejemplo:
=SUMA(B1:B5)
Paso 6: Calcula la desviación estándar
Por último, para obtener la desviación estándar, debes utilizar la fórmula =RAIZ() de Excel y dividir la suma de los cuadrados de las diferencias entre el número total de datos menos 1 y calcular la raíz cuadrada de ese resultado. Por ejemplo:
=RAIZ(SUMA(B1:B5)/(CONTAR(A1:A5)-1))
Una vez que hayas seguido estos pasos, obtendrás el valor de la desviación estándar de tus datos en Excel.
La desviación estándar en Excel es una herramienta útil para analizar la dispersión de datos en un conjunto. Puedes utilizar la función «STDEV» para calcularla de manera sencilla. Recuerda que la desviación estándar nos indica cuánto varían los valores con respecto a la media. Espero que esta información haya sido útil. ¡Hasta luego!